Chi-square distribution

chi-squared

Probability density function
Cumulative distribution function
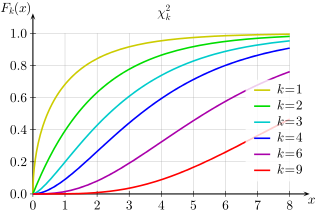
Notation	${\displaystyle \chi ^{2}(k)\;}$ or ${\displaystyle \chi _{k}^{2}\!}$
Parameters	${\displaystyle k\in \mathbb {N} _{>0}~~}$ (known as "degrees of freedom")
Support	${\displaystyle x\in (0,+\infty )\;}$ if ${\displaystyle k=1}$, otherwise ${\displaystyle x\in [0,+\infty )\;}$
PDF	${\displaystyle {\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\;}$
CDF	${\displaystyle {\frac {1}{\Gamma (k/2)}}\;\gamma \left({\frac {k}{2}},\,{\frac {x}{2}}\right)\;}$
Mean	${\displaystyle k}$
Median	${\displaystyle \approx k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}\;}$
Mode	${\displaystyle \max(k-2,0)\;}$
Variance	${\displaystyle 2k\;}$
Skewness	${\displaystyle \scriptstyle {\sqrt {8/k}}\,}$
Ex. kurtosis	${\displaystyle {\frac {12}{k}}}$
Entropy	${\displaystyle {\begin{aligned}{\tfrac {k}{2}}&+\log(2\Gamma (k/2))\\&\!+(1-k/2)\psi (k/2)\,{\scriptstyle {\text{(nats)}}}\end{aligned}}}$
MGF	${\displaystyle (1-2t)^{-k/2}{\text{ for }}t<{\frac {1}{2}}\;}$
CF	${\displaystyle (1-2it)^{-k/2}}$
PGF	${\displaystyle (1-2\log t)^{-v/2}{\text{ for }}0<t<{\sqrt {e}}\;}$

In probability theory and statistics, the chi-squared distribution (also chi-square or χ²-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-square distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, e. g., in hypothesis testing or in construction of confidence intervals. When it is being distinguished from the more general noncentral chi-squared distribution, this distribution is sometimes called the central chi-squared distribution.

The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests also use this distribution, such as Friedman's analysis of variance by ranks.

If Z₁, ..., Z_k are independent, standard normal random variables, then the sum of their squares,