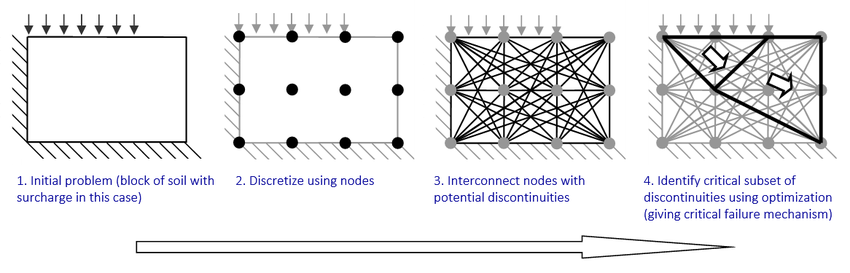
Discontinuity layout optimization

Discontinuity layout optimization (DLO) is an engineering analysis procedure which can be used to directly establish the amount of load that can be carried by a solid or structure prior to collapse. Using DLO the layout of failure planes, or 'discontinuities', in a collapsing solid or structure are identified using mathematical optimization methods (hence the name, 'discontinuity layout optimization'). It is assumed that failure occurs in a ductile or 'plastic' manner.

The DLO procedure involves a number of steps, as outlined below.

The set of potential discontinuities can include discontinuities which crossover one another, allowing complex failure patterns to be identified (e.g. involving ‘fan’ mechanisms, where many discontinuities radiate from a point).

DLO can be formulated in terms of equilibrium relations ('static' formulation) or in terms of displacements ('kinematic' formulation). In the latter case the objective of the mathematical optimization problem is to minimize the internal energy dissipated along discontinuities, subject to nodal compatibility constraints. This can be solved using efficient linear programming techniques and, when combined with an algorithm originally developed for truss layout optimization problems, it has been found that modern computer power can be used to directly search through very large numbers of different failure mechanism topologies (up to approx. 2^{1,000,000,000} different topologies on current generation PCs). A full description of the application of DLO to plane strain problems has been provided by Smith and Gilbert, to masonry arch analysis by Gilbert et al, to slab problems by Gilbert et al, and to 3D problems by Hawksbee et al, and Zhang.

Whereas with finite element analysis (FEM), a widely used alternative engineering analysis procedure, mathematical relations are formed for the underlying continuum mechanics problem, DLO involves analysis of a potentially much simpler discontinuum problem, with the problem being posed entirely in terms of the individual discontinuities which interconnect nodes laid out across the body under consideration. Additionally, when general purpose finite element programs are used to analyse the collapse state often relatively complex non-linear solvers are required, in contrast to the simpler linear programming solvers generally required in the case of DLO.

...
Wikipedia