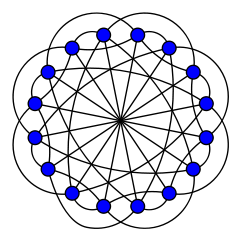
Greenwood–Gleason graph
| Clebsch graph | |
|---|---|
 |
|
| Named after | Alfred Clebsch |
| Vertices | 16 |
| Edges | 40 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 1920 |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Properties |
Strongly regular Hamiltonian Cayley graph Vertex-transitive Edge-transitive Distance-transitive. |
In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge variant is the order-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the order-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.
The order-5 folded cube graph (the 5-regular Clebsch graph) may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an n-dimensional hypercube, a pair of vertices are opposite if the shortest path between them has n edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by identifying together (or contracting) every opposite pair of vertices.
Another construction, leading to the same graph, is to create a vertex for each element of the finite field GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a perfect cube.
The order-5 halved cube graph (the 10-regular Clebsch graph) is the complement of the 5-regular graph. It may also be constructed from the vertices of a 5-dimensional hypercube, by connecting pairs of vertices whose Hamming distance is exactly two. This construction is an instance of the construction of Frankl–Rödl graphs. It produces two subsets of 16 vertices that are disconnected from each other; both of these half-squares of the hypercube are isomorphic to the 10-regular Clebsch graph. Two copies of the 5-regular Clebsch graph can be produced in the same way from a 5-dimensional hypercube, by connecting pairs of vertices whose Hamming distance is exactly four.
...
Wikipedia
