Hypercube graph
| Hypercube graph | |
|---|---|
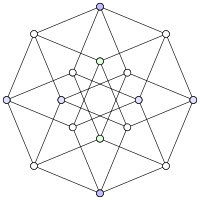
The hypercube graph Q4
|
|
| Vertices | 2n |
| Edges | 2n−1n |
| Diameter | n |
| Girth | 4 if n ≥ 2 |
| Automorphisms | n! 2n |
| Chromatic number | 2 |
| Spectrum | |
| Properties |
Symmetric Distance regular Unit distance Hamiltonian Bipartite |
| Notation | Qn |
In graph theory, the hypercube graph Qn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cubical graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n−1n edges, and is a regular graph with n edges touching each vertex.
The hypercube graph Qn may also be constructed by creating a vertex for each subset of an n-element set, with two vertices adjacent when their subsets differ in a single element, or by creating a vertex for each n-digit binary number, with two vertices adjacent when their binary representations differ in a single digit. It is the n-fold Cartesian product of the two-vertex complete graph, and may be decomposed into two copies of Qn − 1 connected to each other by a perfect matching.
Hypercube graphs should not be confused with cubic graphs, which are graphs that have exactly three edges touching each vertex. The only hypercube graph Qn that is a cubic graph is the cubical graph Q3.
The hypercube graph Qn may be constructed from the family of subsets of a set with n elements, by making a vertex for each possible subset and joining two vertices by an edge whenever the corresponding subsets differ in a single element. Equivalently, it may be constructed using 2n vertices labeled with n-bit binary numbers and connecting two vertices by an edge whenever the Hamming distance of their labels is one. These two constructions are closely related: a binary number may be interpreted as a set (the set of positions where it has a 1 digit), and two such sets differ in a single element whenever the corresponding two binary numbers have Hamming distance one.
...
Wikipedia

