Smoothsort
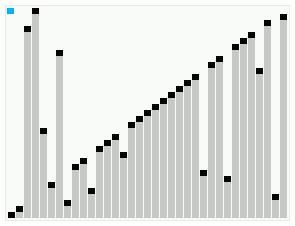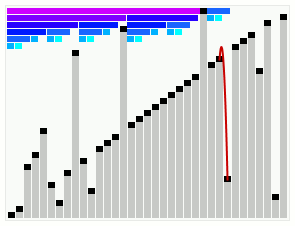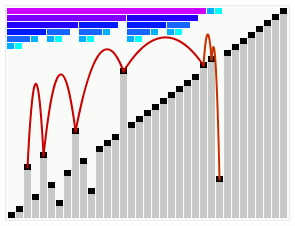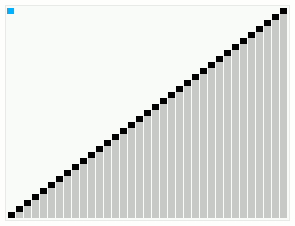
Smoothsort operating on an array which is mostly in order. The bars across the top show the tree structure.
|
|
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(n log n) |
| Best-case performance | O(n) |
| Average performance | O(n log n) |
| Worst-case space complexity | O(n) total, O(1) auxiliary |
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.
Like heapsort, smoothsort builds up an implicit heap data structure in the array to be sorted, then sorts the array by repeatedly extracting the maximum element from that heap. Unlike heapsort, which places the root of the heap and largest element at the beginning (left) of the array before swapping it to the end (right), smoothsort places the root of the heap at the right, already in its final location. This, however, considerably complicates the algorithm for removing the rightmost element.
Dijkstra's formulation of smoothsort does not use a binary heap, but rather a custom heap based on the Leonardo numbers. As he pointed out in his original paper, it is also possible to use perfect binary trees (of size 2k−1) with the same asymptotic efficiency, but there is a constant factor lost in efficiency due to the greater number of trees required by the larger spacing of permissible sizes.
The Leonardo numbers are similar to the Fibonacci numbers, and defined as:
A Leonardo tree of order k ≥ 2 is a binary tree with a root element, and two children which are themselves Leonardo trees, of orders k−1 and k−2. A Leonardo heap resembles a Fibonacci heap in that it is made up of a collection of heap-ordered Leonardo trees.
...
Wikipedia
