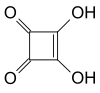
Squaric acid

Squaric acid

Names
IUPAC name 3,4-Dihydroxycyclobut-3-ene-1,2-dione
Other names Quadratic acid
Identifiers
CAS Number	2892-51-5 Y
3D model (JSmol)	Interactive image
ChemSpider	16919 Y
ECHA InfoCard	100.018.875
PubChem CID	17913
InChI InChI=1S/C4H2O4/c5-1-2(6)4(8)3(1)7/h5-6H Y Key: PWEBUXCTKOWPCW-UHFFFAOYSA-N Y InChI=1/C4H2O4/c5-1-2(6)4(8)3(1)7/h5-6H Key: PWEBUXCTKOWPCW-UHFFFAOYAC
SMILES c1(c(c(=O)c1=O)O)O
Properties
Chemical formula	C4H2O4
Molar mass	114.06 g/mol
Appearance	Gray powder
Melting point	> 300 °C (572 °F; 573 K)
Acidity (pKa)	1.5, 3.4
Hazards
R-phrases (outdated)	R36/37/38 R43
S-phrases (outdated)	S26 S36
Flash point	190 °C (374 °F; 463 K)
Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa).
Y  (what is YN ?)
Infobox references

Squaric acid, also called quadratic acid, because its four carbon atoms approximately form a square, is an organic compound with chemical formula C₄H₂O₄.

The conjugate base of squaric acid is the hydrogensquarate anion C₄HO₄⁻; and the conjugate base of the hydrogensquarate anion is the divalent squarate anion C₄O₄²⁻. This is one of the oxocarbon anions, which consist only of carbon and oxygen.

Squaric acid is a reagent for chemical synthesis, used for instance to make photosensitive squaraine dyes and inhibitors of protein tyrosine phosphatases.

Squaric acid is a white crystalline powder with a thermal decomposition point of 245 °C at ambient pressure. The onset of thermal decomposition depends on the different thermodynamic conditions such as heating rates.

The structure of squaric acid is not a perfect square, as the carbon–carbon bond lengths are not quite equal. The high acidity with pK_a = 1.5 for the first proton and pK_a = 3.4 for the second is attributable to resonance stabilization of the anion. Because the negative charges are equally distributed between each oxygen atom, the dianion of squaric acid is completely symmetrical (unlike squaric acid itself) with all C-C and C-O bond lengths identical.

Another, quantum mechanical, way of describing the dianion is to assume that the π electrons of the two double-bonded oxygen atoms are shifted to the latter, so that all four oxygens become single-bonded -O⁻ groups and a double positive electric charge is left in the ring of carbon atoms. In this way the ring fits Hückel's rule for aromaticity (2 π-electrons = 4n + 2 with n = 0). The total symmetry of the dianion is a consequence of charge distribution and aromaticity.