Survivor function

The survival function is a function that gives the probability that a patient, device, or other object of interest will survive beyond any given specified time.

The survival function is also known as the survivor function or reliability function.

The term reliability function is common in engineering while the term survival function is used in a broader range of applications, including human mortality. Another name for the survival function is the complementary cumulative distribution function.

Let T be a continuous random variable with cumulative distribution function F(t) on the interval [0,∞). Its survival function or reliability function is:

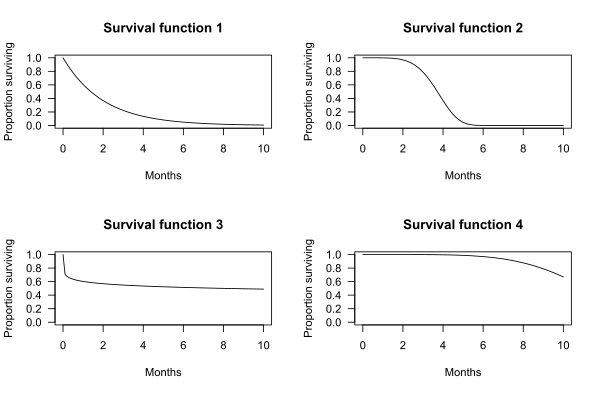
The graphs below show examples of hypothetical survival functions. The x-axis is time. The y-axis is the proportion of subjects surviving. The graphs show the probability that a subject will survive beyond time t.

For example, for survival function 1, the probability of surviving longer than t = 2 months is 0.37. That is, 37% of subjects survive more than 2 months.

For survival function 2, the probability of surviving longer than t = 2 months is 0.97. That is, 97% of subjects survive more than 2 months.

...
Wikipedia