Dürer graph
| Dürer graph | |
|---|---|
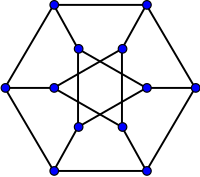
The Dürer graph
|
|
| Named after | Albrecht Dürer |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 3 |
| Automorphisms | 12 (D6) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties |
Cubic Planar well-covered |
In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton. Dürer's solid is one of only four well-covered simple convex polyhedra.
Dürer's solid is combinatorially equivalent to a cube with two opposite vertices truncated, although Dürer's depiction of it is not in this form but rather as a truncated rhombohedron or triangular truncated trapezohedron. The exact geometry of the solid depicted by Dürer is a subject of some academic debate, with different hypothetical values for its acute angles ranging from 72° to 82°.
The Dürer graph is the graph formed by the vertices and edges of the Dürer solid. It is a cubic graph of girth 3 and diameter 4. As well as its construction as the skeleton of Dürer's solid, it can be obtained by applying a Y-Δ transform to the opposite vertices of a cube graph, or as the generalized Petersen graph G(6,2). As with any graph of a convex polyhedron, the Dürer graph is a 3-vertex-connected simple planar graph.
...
Wikipedia
